It is about time to write something on the broader topics I covered in my diploma thesis “Improving a Hierarchical Evolutionary Algorithm with Applications in Optimization and Machine Learning”. Even so, the word Graph does not appear in the title, the thesis was mainly about optimizing graphs, more specifically (spiking) neural networks.
- But what is Evolutionary Graph Optimization actually?
- What is it good for?
- What were the challenges we had to face? (part 2)
- Did we come up with something new? (part 2)
Many questions, to which there are even more answers. In case you are able to understand german language, feel free to read through the 150 pages of my thesis (it covers a lot more than just the four questions above).
To keep you motivated, let’s first take a look at the screenshot below, showing HyperNSGA in action, a graphical software written in Rust that I created as part of the thesis to visualize and interact with the process of evolutionary graph optimization. HyperNSGA is an abbreviation in the style of HyperNEAT and stands for “Hyper-cube based neural net optimization using NSGA-II”, the latter which is again an abbreviation for “Non-Dominated Sorting Genetic Algorithm II”. In the top half of the screenshot, you see the the individual genomes, whereas in the bottom half you see the final networks. The genomes itself are a special kind of graph, so-called Compositional pattern-producing networks or CPPNs. These are smaller networks that we use to produce larger graphs with hierarchical and repetetive patterns. The pane on the right shows settings and performance metrics. Most settings can be modified in real-time, while an optimization is running.
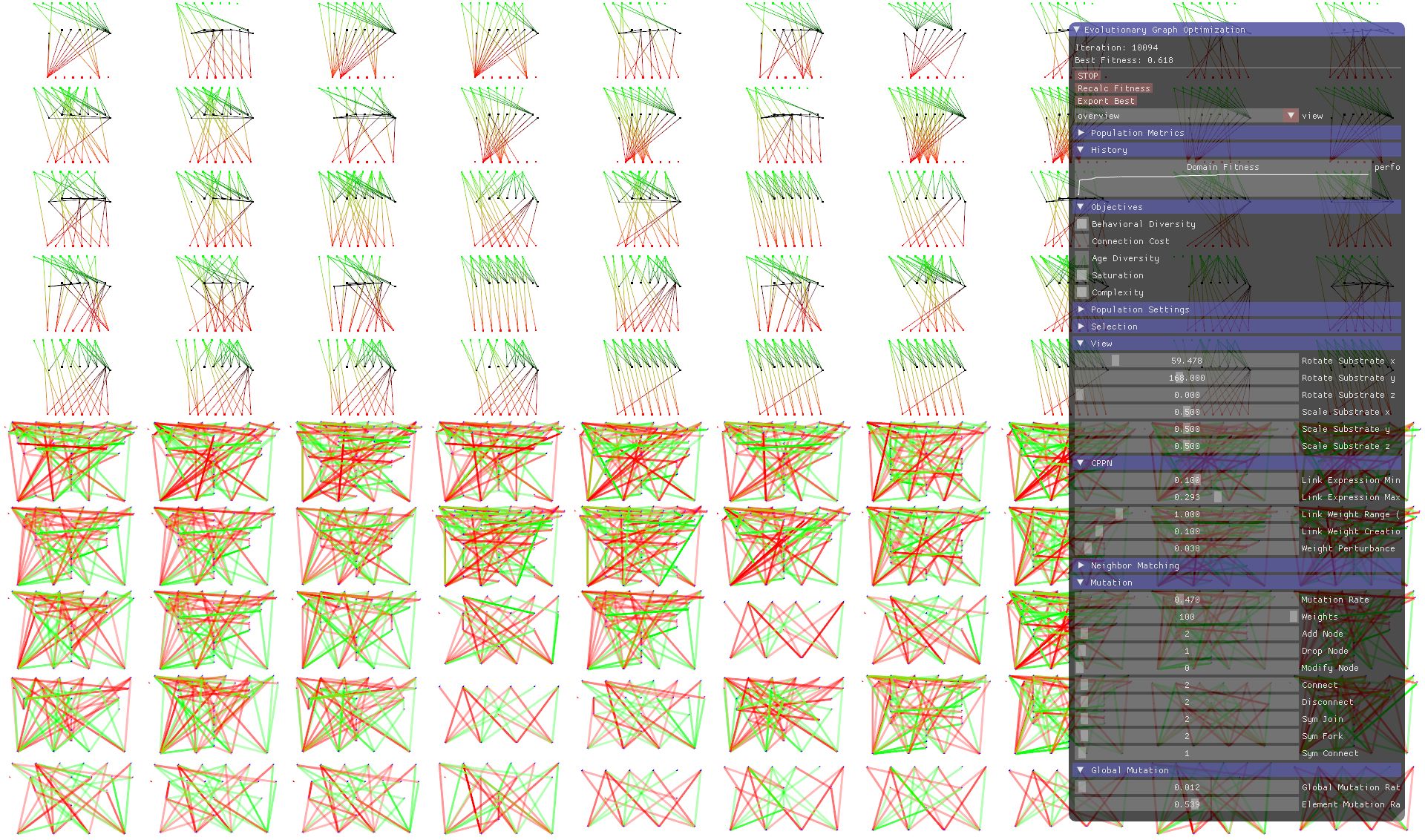
What is Evolutionary Graph Optimization?
Evolutionary algorithms are a class of randomized algorithms, which are more or less based upon Darwin’s theory of biological evolution. They use three concepts: A population of solutions, selection of solutions (“Survival of the Fittest”) and reproduction of new, “child” solutions. The genetic algorithm (GA) is one of the best-known variants of an EA. It uses a binary representation for each solution in the population, called the “genome”, and genetic operators like crossover and mutation to produce new genomes from existing genomes.
In evolutionary graph optimization, we make use of an evolutionary algorithm (EA) to optimize some, or all attributes of a graph. Graphs are made from nodes and edges, both of which can be attributed or weighted. So what a graph optimization algorithm has to accomplish, is to modify the node and edge weights in order to make the graph more “optimal” according to some function, which we call the fitness function. To make things more complex, the fitness function can be multivariate (i.e. not a single scalar value), in which case we are talking about Pareto-optimization. More advanced algorithms not only optimize the weighting of graphs but also modify their topology. The topology is the structure of the graph, the information, which nodes are connected to which other nodes via edges. Optimizing either the weighting or the topology of a graph while keeping the other constant is “easy”, whereas doing both at the same time is a lot more “complex”. What I tried to accomplish in my thesis is to find or develop an algorithm that is able to optimize both, topology and weighting of graphs, at the same time.
What is it good for?
An algorithm that optimizes the topology of a graph can also be used to create graphs. And indeed, the main application for our evolutionary graph optimization algorithm was as a graph generation algorithm.
In our case, we did research on spiking neural networks. Spiking neural networks try to model and simulate biological neural networks, like the ones that make up your nervous system (brain, medulla, etc.). In contrast to artificial neural networks (buzz word “deep learning”), the propagation of signals between connected neurons in spiking neural networks is not immediate, it takes time. This timing contains further information, for instance, the “phase” of a signal, and resembles the biological behavior. The actual biological behavior is a very complex electro-chemical physiological interaction and there are mathematical models, like the Hodgkin-Huxley model, that model the processes inside biological neurons (the flow of ions in both directions through the cell membrane). Obviously, this requires a lot of computational power, so that scientists have invented alternative mathematical models. The one I have chosen was the model of Izhikevich, which is biologically plausible, very well described in numerous papers, easy to implement correctly and most importantly, computational efficient.
Spiking neural networks would be perfect if we would only know how to create them. While crafting small networks by hand is a challenge, for larger networks, this becomes an impossible undertaking. Because of that, artificial neural networks use a regular, often fully-connected, multi-layered topology, and back-propagation to “tune” the synapse weights. With spiking neural networks, this is just not possible. While you can use a layered topology, you would still have to tune the synaptic delays. And what about multiple connections between two neurons with different delays? It started in the 1990’s, when researchers first employed evolutionary algorithms to create and optimize those networks. But they quickly realized that by using simple genetic algorithms, too soon you run into limits, as the search-space explodes exponentially (you can optimize graphs with less than 100 nodes this way).
In short: Evolutionary graph optimization can be employed to create and optimize any kind of attributed graph, in our case, spiking neural networks. Spiking neural networks itself can be used for classification of data, in the same way as artifical neural networks are widely used today.
Next up
In the second part of this article I will talk about the challenges we had to face and whether we came up with new solutions.